Trigonometri, regulære mangekantar og stjerner
Trigonometri, regulære mangekantar og stjerner
Skrevet av: Sigmund Hansen
Oversatt av: Stein Olav Romslo
Introduksjon
No som du kan teikne mangekantar (viss du ikkje har gjort oppgåva om mangekantar bør du gjere den fyrst), skal me sjå på ein spesiell type mangekantar: dei regulære mangekantane. Det vil seie dei mangekantane der lengda av kvar side er lik, og vinkelen i kvart hjørne er lik. Me skal dessutan teikne nokre av dei nære slektningane deira: dei regulære stjernene.
Det er ein stor fordel om du kan litt trigonometri før du startar med denne oppgåva, men me skal prøve å gi korte forklaringar slik at du kan kome gjennom sjølv om du ikkje gjer det.
Sinus og cosinus
For me startar å teikne, så skal me sjå på to trigonometriske funksjonar me kjem til å bruke mykje: sinus og cosinus. Me skal spesielt sjå på dei i samband med sirklar.
- Eit kvart punkt på ein sirkel befinn seg like langt frå midten av sirkelen. Denne avstanden er radius i sirkelen, som regel forkorta
ri figurar og formlar.
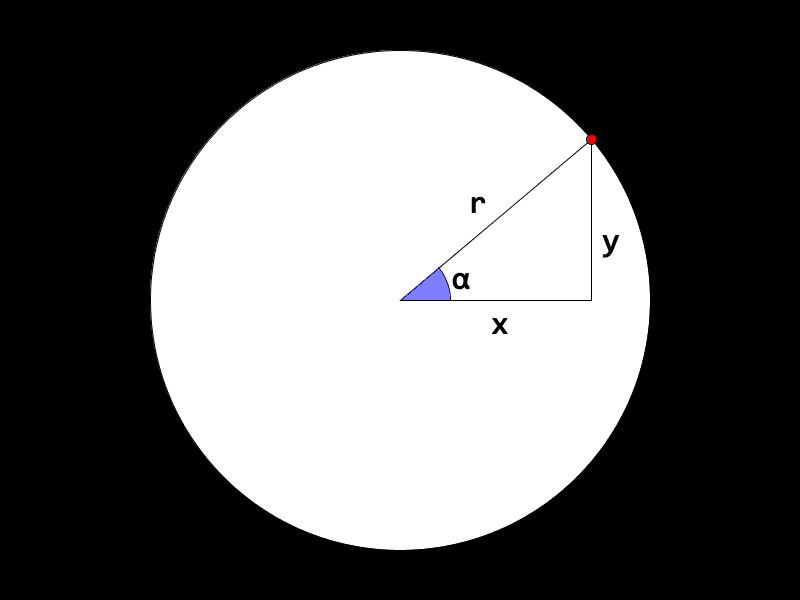
- Me kan teikne ein rettvinkla trekant som ligg vassrett og strekk seg frå sentrum til sirkelbogen.
-
Viss me seier at sentrum av sirkelen ligg i punktet
(0, 0), altså at X og Y er 0 i midten, så kan me enkelt rekne ut X og Y for punktet på sirkelen. To av sidene i trekanten viser då X og Y. Den siste sida er linja frå sentrum med lengder. Difor har me kalla sidenex,yogr: me kan bruke namna for lengdene til sidene òg. For vinklar er det vanleg å bruke greske bokstavar, og her har me bruktα, alfa. -
Lengda på sidene
xogykan me finne med funksjonane sinus og cosinus, vinkelenαogr, altså radiusen til sirkelen. Dei korte sidene som saman lagar det rettvinkla hjørnet kallast katetar, og den lange sida med lengdarkallast hypotenus. Lengda på kateten som er med på hjørnet med vinkelenαhar lengdacos(α) * r. Denne kateten kallast gjerne den hjåliggande kateten. På bokmål kan du skrive hugseregelen "hos blir cos" for å hugse kva side som brukar cosinus-funksjonen. Lengda på den andre kateten, kalla den motståande kateten, ersin(α) * r.
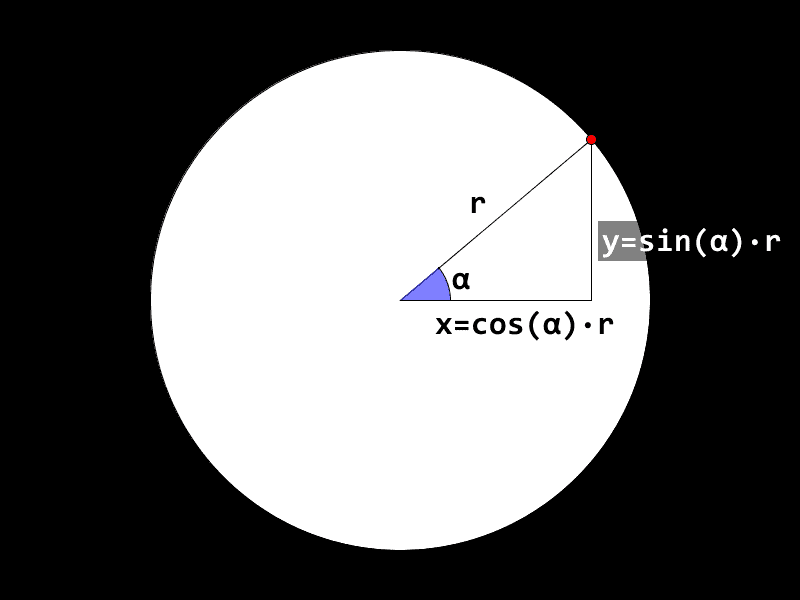
- Det virkar kanskje merkeleg når du berre får formlane på denne måten. Men dei er altså definert slik at sinus og cosinus gir forholdet mellom hypotenusen og katetane:
sin(α) = y / rogcos(α) = x / r. Me skal ikkje sjå på korleis ein finn desse tala ut frå vinkelen, det skal datamaskina gjere for oss!
Regulære mangekantar
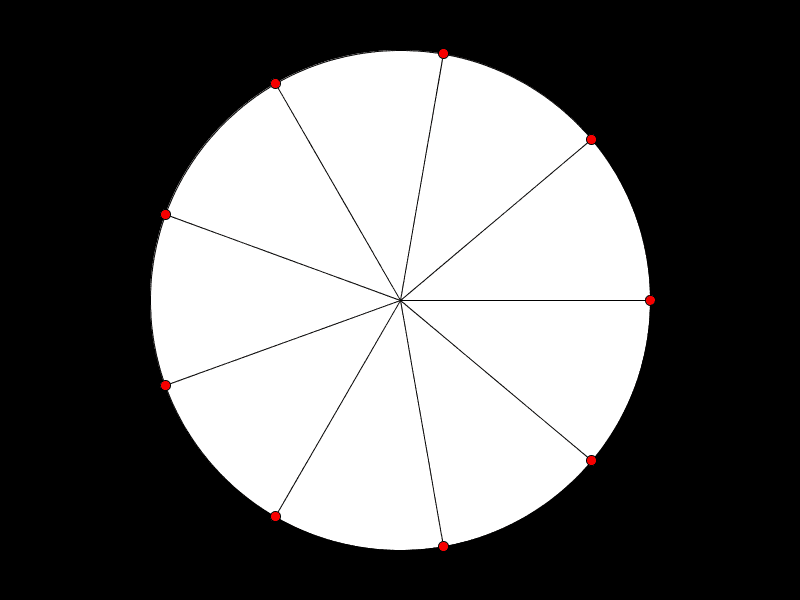
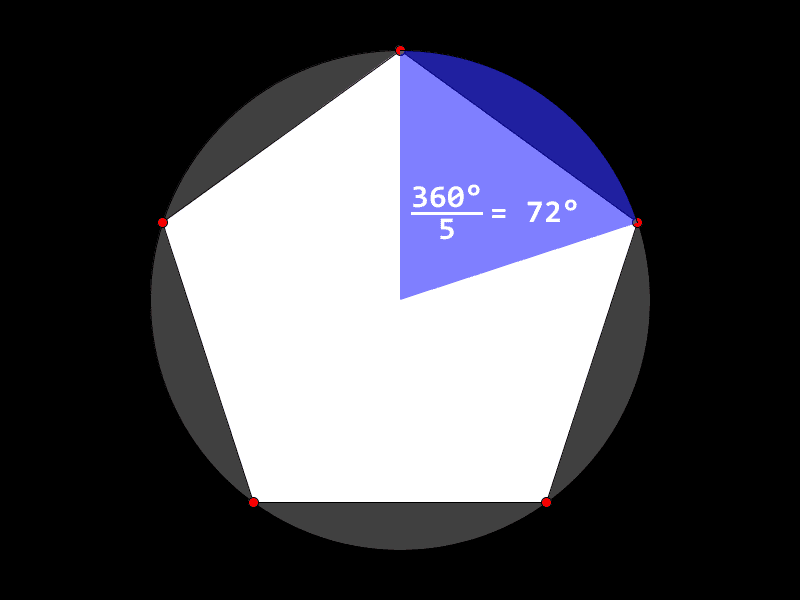
No skal me teikne nokre regulære mangekantar. Det vil seie mangekantar der avstanden mellom kvart hjørne er lik, altså er dei likesida, og vinkelen i kvart hjørne er lik, altså er dei likevinkla. Du lurar kanskje på korleis du skal få til dette. Hjørnene i ein regulær mangekant fordeler seg jamnt langs ein sirkel. Difor kan me bruke formlane for katetane til å reikne ut kor hjørna skal vere. Elles teiknar med figuren akkurat som alle andre mangekantar, slik du gjorde i ei anna oppgåve.
-
int KANTAR = 5; float vinkel = 360.0 / KANTAR; void setup() { size(600, 600); } void draw() { background(0); beginShape(); for (int hjorne = 0; hjorne < KANTAR; hjorne++) { vertex(300 + cos(radians(vinkel * hjorne)) * 200, 300 + sin(radians(vinkel * hjorne)) * 200); } endShape(CLOSE); }Inne i kallet på
vertexser du nokre nye utrekningar. Her brukar me tre nye funksjonar. Funksjonanesinogcosvart forklart lengre opp. Me brukarradiansfor å rekne om gradar til radianar, ei anna måleeining for vinklar.I dataprogram brukar sinus og cosinus vanlegvis radianar, så viss me vil jobbe med vinklar i gradar må me gjere denne konverteringa. Du ser at me har med ein variabel for vinkelen mellom kvart punkt, og den har me berekna i gradar ut frå at ein sirkel er 360°.
Til slutt fortel
CLOSEiendShapeat siste kant i figuren skal setjast saman med den fyrste, altså at me lukkar og fyller figuren.

Regulære stjerner 1
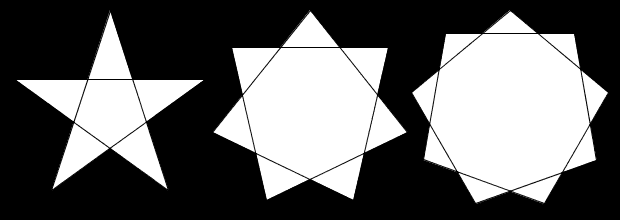
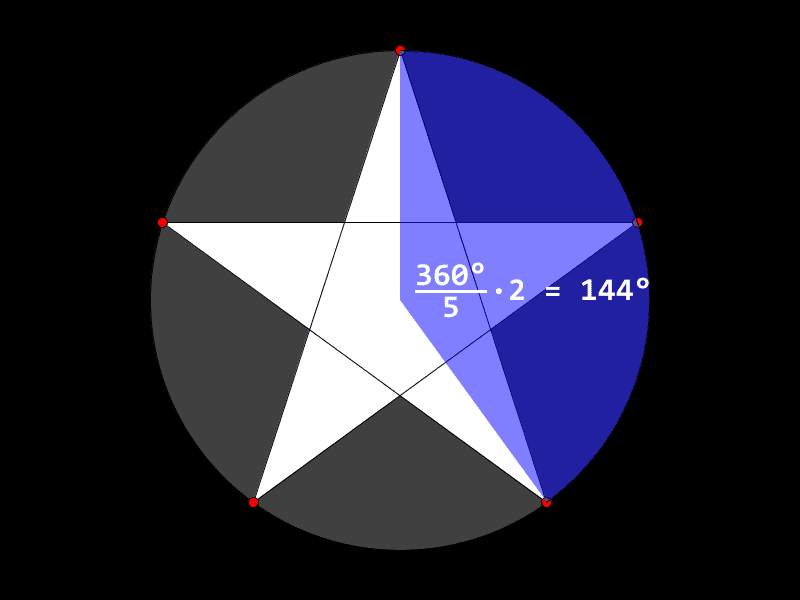
Regulære stjerner med eit odde antal spissar kan teiknast nesten heilt likt som ein teiknar ein regulær mangekant. Dei er på ein måte ein slags variant av mangekantar. Viss du har teikna ei femkanta stjerne før, så har du kanskje lagt merke til at det liknar på ein femkant, men at du hoppar over eit hjørne når du teiknar streken mellom to spissar.
-
vertex(300 + cos(radians(vinkel * hjorne * 2)) * 200, 300 + sin(radians(vinkel * hjorne * 2)) * 200);Kunne du ganga med
2ein annan stad i koden og fått den same effekten?
Regulære stjerner 2
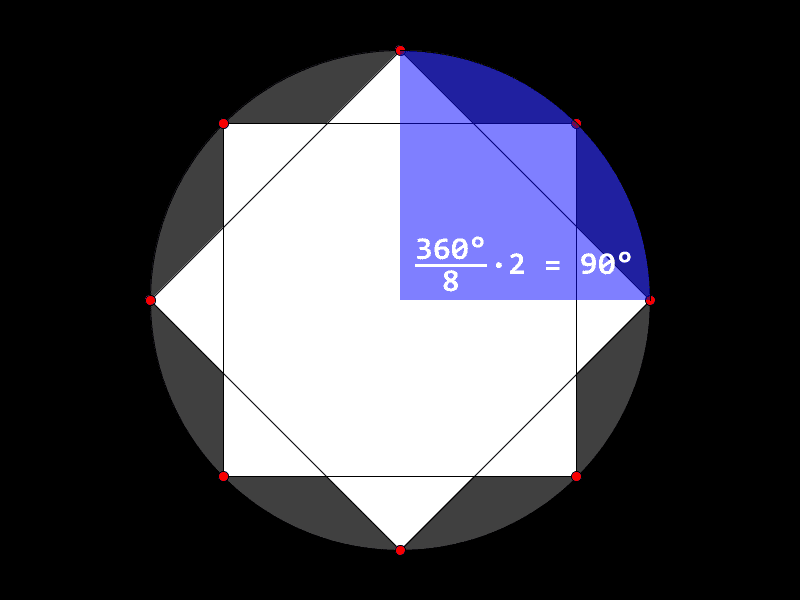
Stjerner med likt antal spissar (altså at det er eit partal) kan bli teikna som to regulære mangekantar med halvparten så mange hjørne som stjerna har spissar.
Utfordring
Forbedre denne siden
Funnet en feil? Kunne noe vært bedre?
Hvis ja, vennligst gi oss tilbakemelding ved å lage en sak på Github eller fiks feilen selv om du kan. Vi er takknemlige for enhver tilbakemelding!