 Skilpaddefraktaler
Skilpaddefraktaler
Skrevet av: Geir Arne Hjelle
Introduksjon
Vi vil nå jobbe videre med skilpaddekunsten fra tidligere. Denne gangen skal vi tegne forskjellige figurer som kalles fraktaler. Fraktaler er figurer som bygges opp av små kopier av seg selv. I løpet av leksjonen vil vi også jobbe mer med funksjoner og rekursjon.

Steg 1: Husker du skilpadden?
Vi har brukt skilpaddebiblioteket turtle tidligere. Du husker kanskje kode som lignet på den under?
from turtle import *
shape('turtle')
shapesize(2)
bgcolor('darkblue')
color('yellow')
speed(3)
forward(270)
 Sjekkliste
Sjekkliste
Steg 2: En fraktal
En fraktal er en figur som er bygd opp av mindre kopier av seg selv. Vi skal nå se på hvordan vi kan tegne denne figuren:

Dette er en fraktal, klarer du å se at den består av mange små kopier av seg selv? Det er kanskje lettere å se i de neste figurene?
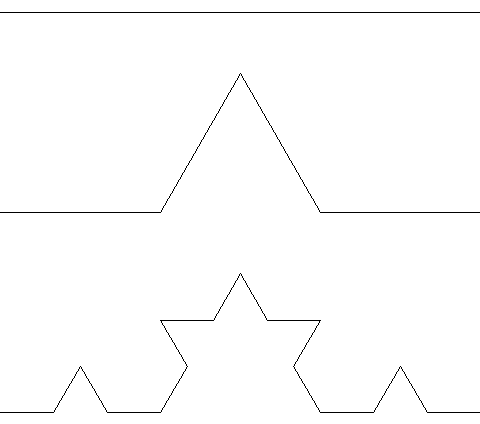
Den øverste figuren er bare en rett strek. Den neste figuren består av fire rette streker som danner et enkelt fjell. Hvis du nå ser nærmere på den tredje figuren ser du at den består av fire kopier av det enkle fjellet, igjen lagt slik at de danner et litt mer komplisert fjell.
Hvis du nå ser tilbake på den første figuren, ser du hvordan den består av mange små kopier av slike fjell?
Steg 3: Vi tar det stegvis
Vi skal se på hvordan vi kan lage funksjoner som kan tegne figurene over.
 Sjekkliste
Sjekkliste
-
from turtle import * shape('turtle') shapesize(2) bgcolor('darkblue') color('yellow') speed(3) def en(): forward(270) en()Husk at vi må kalle funksjonen for at den skal bli gjort.
-
def to(): forward(90) left(60) forward(90) right(120) forward(90) left(60) forward(90) to()Ser du sammenhengen mellom figuren og koden?
-
La oss endre litt i funksjonene slik at vi bruker
eni stedet forforwardnår vi definererto.def en(lengde): forward(lengde) def to(lengde): en(lengde / 3) left(60) en(lengde / 3) right(120) en(lengde / 3) left(60) en(lengde / 3) to(270) -
def tre(): forward(30) left(60) forward(30) right(120) forward(30) left(60) forward(30) left(60) forward(30) left(60) forward(30) right(120) forward(30) left(60) forward(30) right(120) forward(30) left(60) forward(30) right(120) forward(30) left(60) forward(30) left(60) forward(30) left(60) forward(30) right(120) forward(30) left(60) forward(30) -
Hvis du ser litt nærmere på koden vil du se at linjene
forward(30) left(60) forward(30) right(120) forward(30) left(60) forward(30)går igjen flere ganger. Sammenlign disse linjene med funksjonen
tofra tidligere. Ser du en måte vi kan forenkle koden vår? -
def tre(lengde): to(lengde / 3) left(60) to(lengde / 3) right(120) to(lengde / 3) left(60) to(lengde / 3) tre()
Steg 4: Her kan vi kombinere
Nå skal vi lage en funksjon som kan tegne alle tre figurene!
 Sjekkliste
Sjekkliste
Nå kommer det morsomste. Før vi kaster bort tid på å lage flere funksjoner fire, fem og kanskje seks, skal vi se at vi kan lage en funksjon som kan lage alle disse for oss!
Vi skal nå bruke noe som kalles rekursjon for å lage en funksjon som gjør jobben til både en, to og tre. Rekursjon husker du kanskje fra tidligere. Det betyr at vi lager en funksjon som kaller seg selv, men for å gjøre noe som er litt enklere.
Med rekursjon ser man gjerne på det enkle tilfellet og det generelle tilfellet. For disse figurene er en det enkle tilfellet hvor vi bare trenger å tegne en rett strek.
-
def fjell(lengde, dybde): if dybde == 1: forward(lengde) returnHer bruker vi
returnfor å si at vi ikke vil gjøre mer for det enkle tilfellet. -
def fjell(lengde, dybde): if dybde == 1: forward(lengde) return fjell(lengde / 3, dybde - 1) left(60) fjell(lengde / 3, dybde - 1) right(120) fjell(lengde / 3, dybde - 1) left(60) fjell(lengde / 3, dybde - 1)Kjenner du igjen koden fra tidligere?
-
fjell(270, 2)og
fjell(270, 3)Gir dette samme resultat som
to(270)ogtre(270)?
Steg 5: Et snøflak
Vi skal nå kombinere flere slike fjell til et fint snøflak.
 Sjekkliste
Sjekkliste
-
Legg til denne funksjonen:
def snoflak(lengde, dybde): for i in range(3): fjell(lengde, dybde) right(120)
Dette snøflaket er en av de mest kjente fraktalene. Det har fått navnet Kochs snøflak fordi en av de første som studerte denne figuren het Helge von Koch.
Steg 6: Firkantede fjell
La oss se på en variant av snøflaket.
 Sjekkliste
Sjekkliste
Vi vil nå lage en fraktal på samme måte som Koch-figuren men med en litt form. I stedet for en trekant som danner fjellet vil vi bruke en firkant som i figuren under:
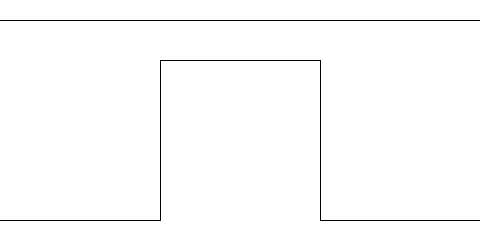
-
from turtle import * shape('turtle') shapesize(2) bgcolor('darkblue') color('yellow') speed(3) def en(lengde): forward(lengde) def to(lengde): en(lengde / 3) left(90) en(lengde / 3) right(90) en(lengde / 3) right(90) en(lengde / 3) left(90) en(lengde / 3) to(270) -
Prøv selv om du kan skrive denne. Se på hvordan vi laget
fjelltidligere, og på hvordan vi lagetenogtonå sist.def firkantfjell(lengde, dybde): if dybde == 1: # Her må du programmere det enkle tilfellet return # Her må du programmere det generelle tilfellet -
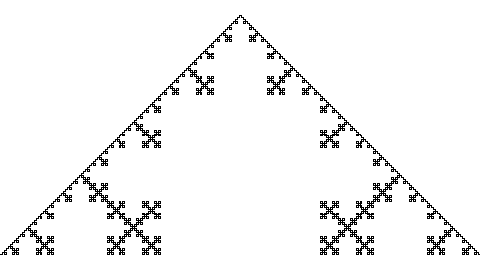
Steg 7: Trekanter
Vi trenger ikke bare bruke rette streker for det enkle tilfellet.
 Sjekkliste
Sjekkliste
Vi skal nå lage en fraktal basert på trekanter. La oss se på de første stegene:
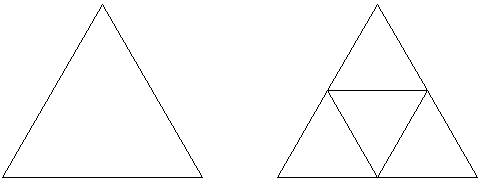
Her ser vi at vi har en trekant som byttes ut med tre mindre trekanter.
-
def trekant(lengde, dybde): if dybde <= 1: pendown() for i in range(3): forward(lengde) left(120) penup() return -
trekant(lengde / 2, dybde - 1) forward(lengde / 2) trekant(lengde / 2, dybde - 1) left(120) forward(lengde / 2) right(120) trekant(lengde / 2, dybde - 1) right(120) forward(lengde / 2) left(120)
Prøv selv
Det finnes mange fraktaler, og du kan lage dine helt egne også!
Prøv for eksempel å endre litt på vinklene og lengdene i fjell- eller firkantfjell-funksjonene.
Eller kanskje du kan lage en helt annen figur? Prøv og tegn dine egne en- og to-figurer som du så oversetter til Python.
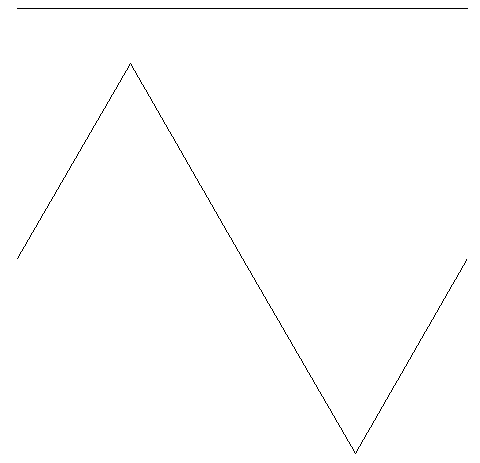
Her er et forslag til en figur du kan prøve, men prøv også å lage dine egne!
Forbedre denne siden
Funnet en feil? Kunne noe vært bedre?
Hvis ja, vennligst gi oss tilbakemelding ved å lage en sak på Github eller fiks feilen selv om du kan. Vi er takknemlige for enhver tilbakemelding!








